728x90
이번 포스트에서는 이진 트리에 대해 다루도록 하겠습니다.
트리란?
: 트리는 1개 이상의 노드로 이루어진 유한 집합으로서 큐나 스택과 같은 선형 구조가 아닌 비선현 자료구조입니다.
트리의 특징 :
- 하나의 루트 노드를 가진다.
- 모든 노드는 0개 이상의 자식 노드를 가진다.
- 노드의 서로간을 연결하는 간선(Edge)이 존재한다.
트리에 관한 용어 정리 :
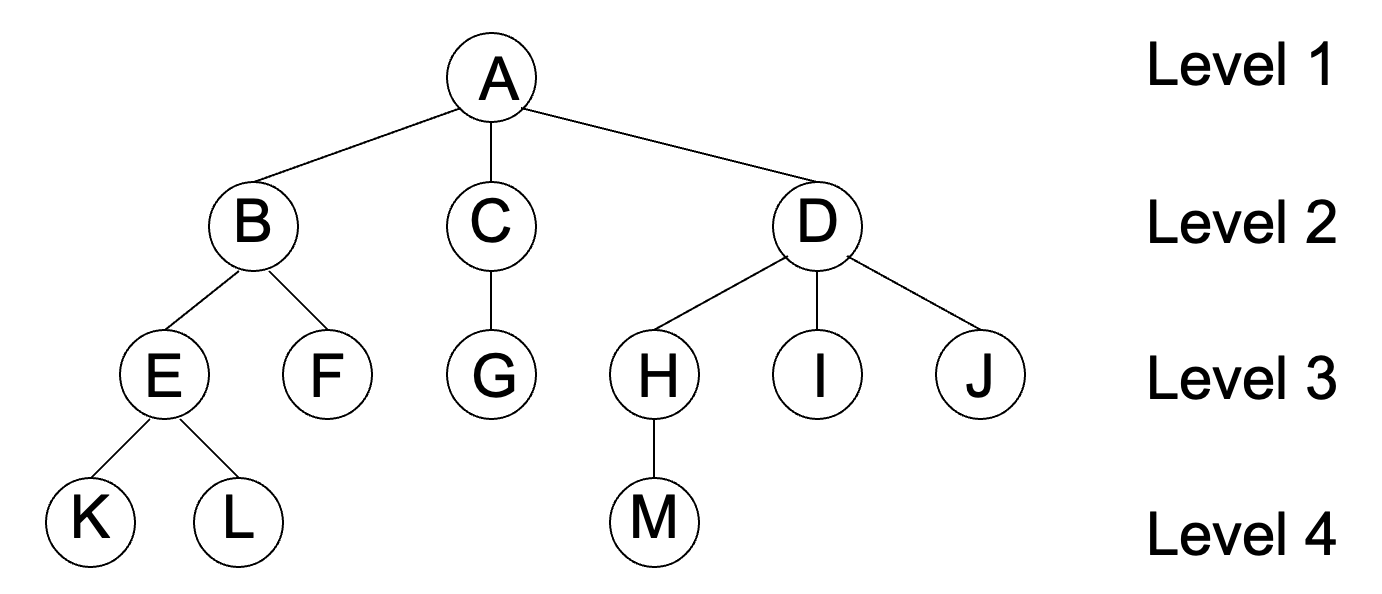
- 노드의 차수(degree) : 자식 노드의 개수 (A : 3)
- 트리의 차수(degree of tree) : 트리의 최대 차수, 즉 제일 많은 가짓수 (3)
- 단말 노드(leaf of terminal node) : 자식이 없는 노드 (K, L, F, G, M, I, J)
- Parent : 부모 노드 (E : B, B : A)
- Children : 자식 노드 (B : E & F)
- Siblings : 같은 부모를 갖는 형제 노드 (E & F)
- Ancestor : 선조 노드 (M : H, D, A)
- Descendants : 후손 노드 (B : E, F, K, L)
- Level : 트리의 특정 깊이를 가지는 노드들의 집합(Level 1 : A, Level 2 : B, C, D)
- Height or Depth : 해당 트리의 루트의 높이(4)
트리의 표현 (그림 1 기준) :
- 리스트 표현 : (A(B(E(K, L), F), C(G), D(H(M), I, J)))
- Left-Child Right-Sibling 표현 : n차 트리의 이진화 표현법, 즉 트리의 모든 노드마다 2개의 링크 필드만 포함

- 왼쪽은 자식 노드, 오른쪽은 형제 노드로 표현 (H의 왼쪽 M은 자식, 오른쪽 I, J는 형제)
이진 트리란?
: 공백이거나 루트 노드, 왼쪽 서브트리, 오른쪽 서브트리라고 하는 2개의 분리된 이진 트리로 구성된 노드의 유한 집합입니다.
이진 트리의 특징 :
- 모든 노드의 차수(degree)는 2를 넘지 않는다.
- 왼쪽 서브트리와 오른쪽 서브트리가 구분된다.
- 이진 트리는 0개의 노드를 포함할 수도 있다.
- 레벨 a에서 최대 노드의 수는 2ª - 1이다 (a ≥ 1)
이진 트리와 일반 트리의 차이점을 간단히 정리하자면 다음과 같습니다.
| 일반 트리 | 이진 트리 |
| 0개의 노드를 가진 트리 X | 0개의 노드를 가진 트리 O |
| 자식의 순서 구분 X | 자식의 순서 구분 O |
완전 이진 트리 :
- 마지막 레벨을 제외한 나머지 레벨이 완전히 채워져 있다.
- 노드가 왼쪽에서 오른쪽으로 채워져야 한다.

포화 이진 트리 :
- 모든 레벨이 노드로 꽉 채워져 있다.
- 모든 노드가 0개 혹은 2개의 자식 노드를 갖는다.
- 트리의 개수가 정확히 2ª - 1개여야 한다. (a = Level)

'Algorithm' 카테고리의 다른 글
| 너비 우선 탐색(Breadth-First Search) (0) | 2022.04.23 |
|---|---|
| 그래프 표현법(인접 행렬, 인접 리스트) (0) | 2022.04.22 |
| 그래프 (Graph) (0) | 2022.04.21 |
| 힙(Heap) (0) | 2022.04.19 |
| 이진 트리 순회 (0) | 2022.04.18 |
