이번 포스트에서는 Cohen-Sutherland(C-S) 알고리즘에 다뤄보겠습니다. 우선 C-S 알고리즘에 어디에서 쓰이는지, 왜 쓰이는지에 대해 소개하겠습니다.
Cohen-Sutherland Algorithm
C-S 알고리즘은 Clipping Algorithm 중의 하나며 2차원 공간을 9개의 영역으로 나누고 화면에서 사용자에게 보여주는 화면 부분을 정해주는 알고리즘입니다.
C-S 알고리즘은 먼저 다음의 기준으로 영역을 나눕니다.

- 1 : Top (위쪽)
- 2 : Bottom (아래쪽)
- 3 : Right (오른쪽)
- 4 : Left (왼쪽)
이 기준을 4-Bit region outcodes이라고 하며, 실제 화면에서 적용하면 다음과 같은 결과를 얻어낼 수 있습니다.
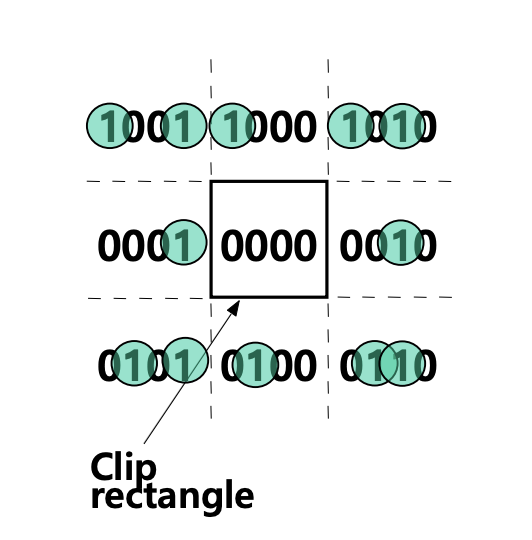
"1001"을 예시로 들자면, 현재 "0000"의 위치 기준으로 봤을 때, "1001"은 "0000"보다 위쪽에 위치하니까 첫번째 비트가 True(1), 또한 왼쪽에 위치하니까 네번째 비트도 True(1)이 들어갑니다. 또 "0100"을 예시로 들자면, "0100"은 "0000"보다 아래쪽에만 위치하니까 아래쪽을 뜻하는 2번째 비트만 True(1) 값이 들어가는 것입니다. 여기서 "0000"은 Clip rectangle, 즉 클립된 사각형 화면을 뜻합니다.
다음에 제시된 그림과 같이 Clip 해야 할 상황이 있다고 가정하면, 우리는 Clip의 카테고리를 3가지로 나눌 수 있습니다.

- Trivially accepted : 두 끝점이 Clip rectangle의 내부에 있을 경우, 즉 선분 전체가 화면 안에 있을 경우 (AB)
- Clipped : 한 끝점이 Clip rectangle의 내부에 있고 나머지 끝점이 외부에 있을 경우, 또는 두 끝점이 동시에 외부에 있을 경우 (CD, GH)
- Trivially rejected : 두 끝점이 Clip rectangle의 외부에 있을 경우, 즉 선분 전체가 화면 바깥에 있을 경우 (EF, IJ)
이를 4-bit region outcodes로 적용 하면 다음과 같은 결과를 얻어낼 수 있습니다.
- Trivially accepted : 두 끝점이 모두 0인 경우
- Trivially rejected : 두 끝점의 AND 연산 값 중에 하나라도 0이 아닌 경우
선분 EF을 예로 들자면, 점 E는 0001에 위치해 있고, 점 F는 1001에 위치해 있습니다. 이를 AND 연산을 해보면 0001이라는 값을 도출할 수 있고 Trivially rejected에 해당하는 것을 알 수 있습니다.
이어서 C-S 알고리즘의 자세한 동작 방식에 대해 소개하겠습니다.

위에 제시된 그림과 같이 선분 A[0000]D[1001]와 선분 EI가 있습니다. 선분 AD를 Clip하는 동작 과정을 정리하자면 다음과 같습니다.
- AD의 카테고리 계산 A[0000] & D[1001] = [0000], Trivially accept도 Trivially reject도 아닌 Clip 영역에 속한 것을 알 수 있다.
- 양점 A, D 중 하나를 선택, 여기서는 D가 [1001], 즉 Clip rectangle 위에 있으니까 D를 선택한다.
- 점 D에서 선분 AD가 Clip rectangle의 위쪽 라인과의 교차점인 B까지 자릅니다, AD -> AB
결과는 다음 그림과 같습니다.

이어서 선분 E[0100]I[1010]를 보겠습니다. 마찬가지로 C-S 알고리즘의 과정을 적용하면 다음과 같습니다.
- EI의 카테고리 계산 E[0100] & I[1010] = [0000], Trivially accept도 Trivially reject도 아닌 Clip 영역에 속한 것을 알 수 있다.
- 양점 E, I 중 하나를 선택, 여기서는 아무 값이나 선택해도 상관없다, 왜냐하면 양점 다 Clip rectangle의 바깥에 위치하기 때문이다. 그럼 Clip rectangle 밑에 있는 E[0100]를 선택한다.
- 점 E에서 선분 EI가 Clip rectangle의 아래쪽 라인과의 교차점인 F까지 자릅니다, EI -> FI
한 번의 C-S 과정을 거치면 다음과 같은 결과를 얻을 수 있습니다.

그러나 선분 F[0000]I[1010]가 여전히 Clip rectangle의 바깥쪽에 있다는 사실을 우리는 육안으로 확인할 수 있습니다. 그러나 컴퓨터는 육안이 없기 때문에 선분의 카테고리가 Trivially reject될 때까지 계속 알고리즘을 실행한다. 쉽게 말해 방금 했던 과정을 선분이 Clip rectangle 안에 있을 때까지 계속 반복한다는 말입니다.
- FI의 카테고리 계산 F[0000] & I[1010] = [0000], Trivially accept도 Trivially reject도 아닌 Clip 영역에 속한 것을 알 수 있다.
- 양점 F, I 중 하나를 선택, 여기서는 I가 [1010], 즉 Clip rectangle 위에 있으니까 I를 선택한다.
- 점 I에서 선분 FI가 Clip rectangle의 위쪽 라인과의 교차점인 H까지 자릅니다, FI -> FH
- 점 H의 outcode를 계산 -> [0010]
- 양점 F, H의 카테고리 계산 -> [0000], 여전히 Clip 영역에 속하므로 반복.
- 양점 F, H 중 하나를 선택, 여기서는 H가 [0010], 즉 Clip rectangle 오른쪽에 있으니까 H를 선택한다.
- 점 H에서 선분 FH가 Clip rectangle의 오른쪽 라인과의 교차점인 G까지 자릅니다, FH -> FG
- 점 G의 outcode를 계산 -> [0000]
- 이제 양점 F, G의 outcode 중 두 끝점이 모두 0이므로 Trivially accept에 속한다.
마지막으로 Cohen-Sutherland 알고리즘 정리하자면 다음과 같습니다.
- 평면을 9개의 영역으로 나누너 각 영역마다 4비트의 고유 코드를 부여
- 선분의 각 끝점(endpoints)이 위치하는 영역에 따라 코드를 해석하여 클리핑 카테고리를 결정
- 여러 번의 C-S 알고리즘 반복 실행
'Computer Graphics' 카테고리의 다른 글
| Clipping Polygons (다각형 클리핑) (0) | 2022.04.05 |
|---|---|
| Parametric Line Clipping (매개 변수 선분 알고리즘) (0) | 2022.04.03 |
| Filling Polygons (다각형 내부 채우기 알고리즘) (0) | 2022.03.30 |
| Scan Conversion (스캔 변환) (0) | 2022.03.29 |
| Random scan & Raster scan (0) | 2022.03.27 |
