이번 포스트에서는 컴퓨터 그래픽스의 Parametric Line Clipping Algorithm(매개 변수 선분 알고리즘)에 대해 다루도록 하겠습니다.
Parametric Line Clipping Algorithm
지난 포스트에서는 C-S 알고리즘에 대해 다루었습니다. C-S 알고리즘은 선분의 양 끝점이 어디에 위치하느냐에 따라 선분을 accepted, rejected, clipped로 나누어 반복 실행을 통해 구했습니다. Parametric Line Algorithm은 이것을 바탕으로 단 한 번만 자르는 C-S알고리즘보다 더 효율적인 알고리즘이다.
먼저 다음에 제시된 그림을 통해 그래픽스 상의 선분의 특징에 대해 알아보겠습니다.

Line 1, 2, 3이 있습니다. 세 Line의 양 끝점이 각각 P0와 P1입니다. 또한 Line1과 Line2는 윈도우와의 교차점이 2개, Line3는 윈도우와의 교차점이 4개인 것을 눈으로 확인할 수 있습니다. 그러나 만약 Line1의 선분을 무한히 연장해본다고 가정해봅시다. 그럼 Line1은 윈도우와의 교차점이 4개가 되겠습니다. 즉, 모든 선분이 윈도우와 가질 수 있는 교차점의 최댓값이 4개인 것입니다.

그러면 선분이 가질 수 있는 4개의 교차점 중에 실제 윈도우와 교차되는 점은 어떻게 구할 수 있을까?
그림을 자세히 살펴보면 선분의 양 끝점 P0, P1은 각각 t=0, t=1의 값을 가지고 있습니다. 즉 선분의 실제 교차점은 0<t<1의 범위의 값을 가지고 있다는 것을 도출해낼 수 있습니다.
이어서 그 끝점을 가지고 윈도우의 inside인지, outside인지를 구하는 법에 대해 다루겠습니다.

위에 제시된 그림과 같이 선분 P0P1이 있습니다. Edge Ei를 기준으로 오른쪽은 윈도우의 inside, 왼쪽은 윈도우의 outside라고 할 수 있습니다. 각 요소에 대한 설명은 다음과 같습니다.
- Ni : 가장자리의 외측으로 직각으로 뻗어나가는 벡터
- PEi : 가장자리 Ei상의 임의의 한 점
- P(t) - PEi : t값을 이용해 PEi부터 선분 P0P1 상의 지정된 세 점과의 벡터
따라서 우리는 Ni*[P(t) - PEi]의 부호를 통해 간편하게 각 점이 어떤 위치에 있는지를 알아낼 수 있습니다.
- "-" : 윈도우 안쪽
- "0" : 윈도우 가장 자리 위
- "+" : 윈도우 바깥쪽
또한 t값은 Ni*[P(t) - PEi]라는 식을 통해 아래 그림과 같이 구할 수 있습니다.

이렇게 계산된 t값(t는 최대 4개)을 가지고 선분을 자를 수 있습니다. 아래 그림을 같이 살펴보겠습니다.
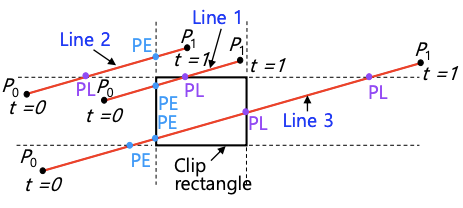
먼저 각 선분 상에서 PE와 PL을 구합니다. 구하는 방법은 다음과 같습니다.
- PE : 끝점 P0에서 끝점 P1로 이동할 때 윈도우 내부로 진입하기 위해 윈도우 경계선(가장자리)과 교차하게 된 점
- PL : 끝점 P0에서 끝점 P1로 이동할 때 윈도우 외부로 나가기 위해 윈도우 경계선(가장자리)과 교차하게 된 점
그 다음에 tE와 tL를 구합니다. 구하는 방법은 다음과 같습니다.
- tE : 가장 큰 t값을 가진 PE
- tL : 가장 작은 t값을 가진 PL
이제 tE와 tL를 가지고 다음 그림과 같이 쉽게 선분을 자를 수 있게 됩니다. 단, 만약 tE > tL인 경우, rejected에 해당하므로 고려하지 않아도 됩니다.

[그림 자료 출처: Introduction to Computer Graphics, Foley]
'Computer Graphics' 카테고리의 다른 글
| Antialiasing (안티에일리어싱) (0) | 2022.04.06 |
|---|---|
| Clipping Polygons (다각형 클리핑) (0) | 2022.04.05 |
| C-S Algorithm (0) | 2022.03.31 |
| Filling Polygons (다각형 내부 채우기 알고리즘) (0) | 2022.03.30 |
| Scan Conversion (스캔 변환) (0) | 2022.03.29 |
