Parametric Cubic Curves (2)

이번 포스트에서는 parametric cubic curves를 좀 더 심화적으로 다루도록 하겠다.

 

곡선을 나타내는 데 사용하는 다항식의 차수는 3차다. 그러기 위해 여러개의 3차 다항식을 연결하는 데 joined 포인트를 사용하게 되는데, 이때, 보다 부드럽게 연결하기 위한 조건은 다음과 같다.

• Parametric Continuity Condition
• Geometric Continuity Condition

Parametric Continuity Condition :

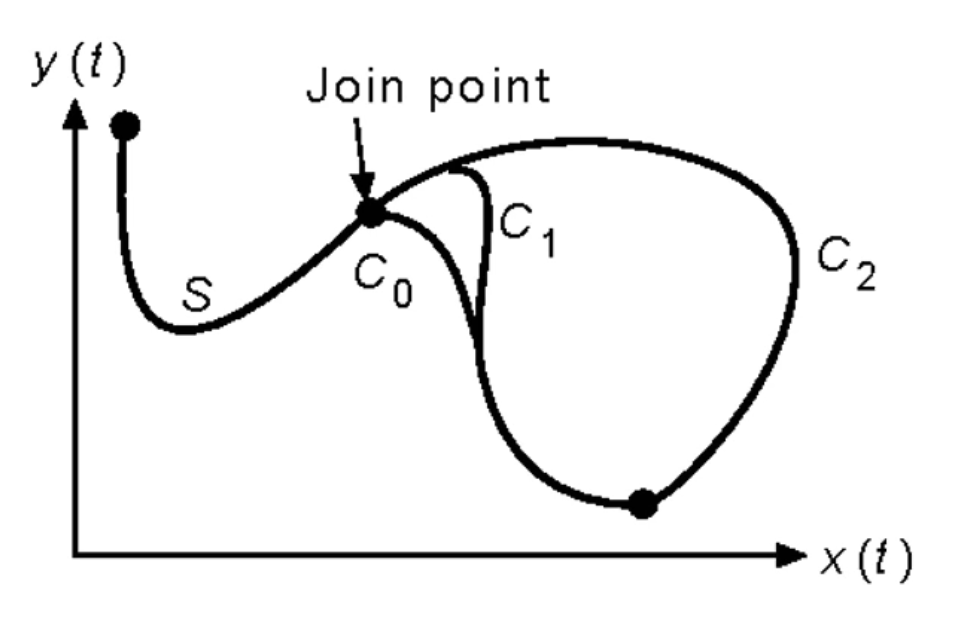
1. Zero-order Parametric Continuity(0차, C0) : 단순히 2개의 곡선 조각이 연결점에서 만나면 된다.
2. First-order Parametric Continuity(1차, C1) : 연결점에서 접선(tangent lines)의 기울기가 같도록 2개의 곡선 조각이 이어지도록 하면 된다.
3. Second-order Parametric Continuity(2차, C2) : 2개의 곡선이 첫 번째와 두 번째 도함수가 모두 교차점에서 같으면 된다. (기울기와 기울기의 변화율이 모두 같아야 함) 주로 애니메이션 경로나 카메라의 이동경로에 쓰인다.

Parametric Continuity Condition을 적용한 그림

 

Geometric Continuity Condition : 

1. G0 geometric continuity : 곡선 조각이 서로 이어지는 연결지점에서 좌표값만 같으면 된다.
2. G1 geometric continuity : 두 조각의 방향(tangent vector)만 같으면 된다.
3. G2 geometric continuity : 두 조각의 방향이 같고 그 기울기의 변화율가 서로 비례하면 된다.

Geometric Continuity Condition과 Parametric Continuity Condition을 동시에 적용한 그림

• TV : Tangent Vector (방향)
• Q1, Q2 : C1의 조건을 만족한 곡선
• Q1, Q3 : G1의 조건을 만족한 곡선

[그림 자료 출처: Introduction to Computer Graphics, Foley]